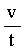1.1
Introduction:
Matter opposes any change in motion. A simple statement that has
perplexed mankind since the dawn of history. Galileo's contribution
was the observation that heavy objects fall at the same rate as
light objects. Newton's contribution was to give mathematical form
and substance to Galileo's observation. By the 19th century, this
picture was completed with the kinetic energy equivalence of matter
in motion. However, two questions have remained unanswered…
1. Exactly where is this energy stored and in what form?
2. How does the storage of this energy cause movement?
These are the question I shall endeavor to answer here.
1.2.1
Acceleration and Force:
Acceleration results from the application of mechanical force to a
mass. Acceleration is nothing more than a measurement of "rate of
change" in velocity.
Where:
And since acceleration results from the application of mechanical
force.
[Eq. 2] F = M a
Where:
Therefore, under constant applied force, the acceleration of any
object is a linear change in velocity over time, of the object.
1.2.2
Kinetic Energy:
The kinetic energy of any moving object, is related to it's motion
by the equation:
[Eq. 3] E = ˝ M v2
Where:
The kinetic energy of any moving object scales proportionally with
the mass of the object, and as the square of it's velocity.
1.3.1
Electro-magnetic Induction:
If we wrap an insulated wire around a paramagnetic substance, we
create an electrical device called an inductor, and a curious
phenomena occurs when an electric current flows through the wire.
The inductor opposes any change in the flow of current. Consider
the circuit shown in figure 1A. Closing the switch, starts the flow
of current through the inductor. However, the inductor opposes any
change in the electric current flow, so the current rises linearly
over time as shown in figure 1B.
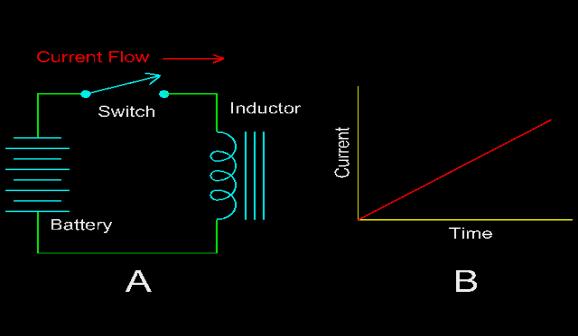
Figure 1
Since current flow is defined as electric charge (Q) per second, or
(Q/t), it follows that figure 1B is describing a change in charge
(Q) per second, per second (per second squared). Therefore in
figure 1 electric charge (Q) is changing as the second derivative of
time, just as in mechanical acceleration [Eq. 1], length is changing
as the second derivative of time. In other words, the flow of
electric charge (Q) is accelerating. We shall use the symbol aQ
to denote accelerated charge, and define it as:
Where:
And since AQ results from the application of electric
potential (force), supplied by the battery, our force equation for
figure 1 is:
[Eq. 5] e = L aQ
Where:
As we see from Eq. 4 & 5, the circuit shown in figure 1A has an
equivalent mathematical form, and exhibits analogous physical
dynamics to mechanical acceleration and force (1.2.1 Eq. 1 & 2).
Note: Dimensional units of the electric field are Newtons per
Coulomb, therefore in the strict sense of the word, an electric
potential is not a "force". The electric field creates a force on
an electric charge.
1.3.2
Inductive Energy:
The inductor shown in figure 1A acts as an energy storage device.
The energy is stored as unpaired electron spin alignments of the
paramagnetic material. This phenomena is known as paramagnetic
polarization. A larger population of unpaired spins, yields a
greater inductance and greater energy storage. The stored
electrical energy of an inductor is related to current flow by the
equation:
[Eq. 6] E = ˝ L i 2
Where:
The electrical energy scales proportionally with the inductance, and
as the square of electric current flow. Again we see an equivalent
mathematical form and analogous physical dynamics to kinetic
(mechanical) energy (1.2.2 Eq. 3).
1.3.3
Matter Flow:
All matter is composed of atoms, that are in turn, composed of
electrons, protons, and neutrons. All of these subatomic particles
are electrically charged (covertly in the case of the neutron).
Therefore we can treat any moving object as an electric current.
Consider an object one meter in length, composed of Q electric
charges, and having a velocity of one meter per second. This object
represents a current flow of:
Where:
By making our object a unit length, we can derive an electric
current flow equivalence to the object's mass and velocity. We
conclude that all moving objects represent flows of electric
current.
1.3.4
Paramagnetic Space:
Space possesses the property of paramagnetic polarization. A
detailed discussion of this subject is available in the companion
paper titled Electrodynamic Structure Space - Parts 1 & 2, and
therefore will not be covered here. Suffice it to say, that empty
space behaves in an equivalent way to a paramagnetic material, and
is capable of storing energy as paramagnetic polarization.
1.4.1
Momentum as Induction:
We have shown that an electrical inductor behaves in a manner that
is fully equivalent to the momentum of physical mass. Electric
charge accelerates through an inductor (1.3.1 Eq. 5) under the
application of an electric force, just as a physical mass
accelerates through space under the application of physical force
(1.2.1 Eq. 2). Energy stored in an inductor is proportional to the
square of current (1.3.2 Eq. 6), just as kinetic energy stored in
mass is proportional to the square of velocity (1.2.2 Eq. 3). We
have also shown that mass is composed of electric charge, and that a
moving mass represents a flow of electric current (1.3.3 Eq. 7).
Lastly we have shown that space is paramagnetic and can be
polarized (1.3.4). Therefore, we have answered question one, posed
above (1.1). The energy of a moving mass results from polarization,
caused by the moving electric charges that comprise the mass, is
magnetic in form, and stored as paramagnetic polarization in the
space occupied by the mass.
1.4.2
Stays in Motion:
Returning to our circuit in figure 1A (above), when the switch is
opened, current flow does not cease instantly. The inductor has
stored energy in the polarization of the paramagnetic material, and
this energy must be dissipated (removed) before current can cease to
flow. An analogous situation exists for any physical mass in
motion. The movement of mass represents an electric current flow
(1.3.3), and that current flow has paramagneticly polarized (stored
energy in) the space through which the mass is moving. If the mass
was to stop moving, without the application of an external force,
this would represent a violation of the law of energy conservation.
Therefore we must remove the energy stored as paramagnetic
polarization of space, by the application of a force in opposition
to motion, in order to dissipate the energy stored in polarization
of space, before the mass will stop moving. We have now answered
question two (1.1) above.
1.4.3
Conclusions:
That momentum is induction (1.4.1), and arises as a consequence of
matter being composed of electric charge, and movement of mass
representing an electric current flow (1.3.3). That kinetic energy
is stored as paramagnetic polarization of space (1.3.4) occupied by
the moving mass. That an object in motion, will remain in motion,
until the energy of paramagnetic polarization is dissipated (1.4.2).
To many readers this may all seem moot, since this formulation of
inductive momentum does not appear to provide any added utility over
the traditional mechanical treatment of the subject. However, when
this formulation is coupled with the companion paper entitled
Electrodynamic Structure of Space, many hitherto poorly understood
relativistic phenomena flow as natural consequences of this
formulation.
End.
Inductive Momentum
|