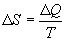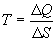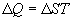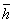2.1.1

Introduction:

In part 1 one we covered the scientific and societal controversy surrounding Maxwell's daemon, and briefly touched on two devices that exhibit anti-entropic behavior.  In part 2 we shall take an in-depth look at the mechanism responsible for anti-entropic behavior in the laser.  This mechanism is called a population inversion, and until the mid twentieth century, was considered little more than a quaint mathematical curiosity, with no basis in physical reality.  In order to lay a proper foundation for discussion of inverted populations, sections 2.1.2 and 2.1.3 are included as a short review of classical thermodynamics.

2.1.2

Degrees of Freedom:

At it's most basic level, the science of thermodynamics is a statistical study of vibration and movement in populations of atoms or molecules.  In order to numerically quantify a population, it is necessary to understand how many different ways or modes of vibration and/or movement are available to the population.  For instance, a population of molecules that have magnetic properties, when under the influence of a magnetic field, may be constrained to movement in a single direction, and yet in the absence of a magnetic field, this same population may have nearly unlimited directions of movement.  In thermodynamics we use the term "degrees of freedom" to describe the number of available modes of vibration and/or directions of movement.  Alternately, degrees of freedom can be viewed as the set of locations available to a population of atoms or molecules when it moves or vibrates.  This set of available locations is called the population's "phase space".

2.1.3:

Temperature, energy, and entropy:

The concept of temperature arose from a need to quantify the human perception of hot and cold.  However at the beginning of the 19th century, no scientist was sure what temperature was really measuring.  It was well known that expending energy (doing work), such as drilling a hole, or bending sheet metal caused the material to get hot, so heat was related to energy in some manner.  But what was heat?  Some believed it was a discrete substance, separate from matter (they called it caloric), while others believed it was an inherent property of matter, like mass or volume.  In 1877, the debate was settled by the mathematician Ludwig Boltzmann.  He showed that heat is a property of matter, directly related to the energy stored in it's vibration and/or movement, AND related to the entropy (disorder) of that vibration or movement.  Unfortunately his theories were met with extreme skepticism by the scientific community of that era (Maxwell was an exception).  Despondent, he later committed suicide.  Had he lived just a few more years, Boltzmann would have seen his theories vindicated beyond his wildest dreams.  Scientific luminaries such as Albert Einstein and Max Planck used Boltzmann's theories in their work.  Work that has shaped modern quantum physics as we know it today.

Boltzmann's controversial equation, Eq. 1 relates the entropy of an atomic or molecular population to it's phase space (disorder).  As a side note, this equation was engraved on his tombstone...

[Eq. 1]    S = k Log W

Where:

Form our perspective, the utility of Eq. 1 is that it defines entropy (disorder) as the ratio of energy to temperature.  Looked at another way, given a population with a constant energy content, as entropy declines, temperature rises.  In other words, as the degrees of freedom available to a population diminish, those few degrees of freedom still available, MUST contain the entire energy content of the population, and this causes the temperature of the population to rise.

Thanks to the genius of Boltzmann, we can define the relationships between temperature, energy, and entropy

as:   [Eq. 2a] [Eq. 2b] [Eq. 2c]   Where:

One last observation is relevant before moving on.  Eq. 2b implies that for any population with a non-zero energy content, as entropy approaches zero (one degree of freedom), the temperature of the population approaches infinity.

2.1.4

Maximum disorder:

Is there an upper limit to disorder?  The answer to this question depends on the degrees of freedom available to a population of atoms or molecules.  For most populations, and in the most general sense of the question, the answer is "no".  This answer has a practical consequence.  It implies there is no upper limit to temperature, since there will always be another dimension in phase space (degree of freedom), to which we can add another increment of energy, and thereby raise the temperature of the population.

However, if a population has a limited set of dimensions in phase space (limited degrees of freedom), there is a definite upper limit to disorder.  Surprisingly, the limit will be reached when exactly half of the dimensions in phase space are occupied by the population.  It is obvious that when a population of atoms or molecules contain no energy, they do not vibrate or move, and therefore all members of the population occupy a single point in phase space (no disorder).  Now consider the opposite condition.  I.E. Every member of the population is vibrating or moving in every available degree of freedom (all dimensions of phase space are occupied).  Again, all members of the population are exactly alike, and again there is no disorder.  Therefore maximum disorder (and entropy) is achieved when exactly 50% of the dimensions in phase space are occupied.  As a consequence of this remarkable situation Eq. 2b implies the temperature of a population at maximum disorder is infinite, and the temperature of any population where more than 50% of phase space is occupied is negative AND hotter than infinity.  Figure 1 shows the relationship between temperature and phase space occupancy for a population with limited degrees of freedom.

2.2.1

Quantum populations:

While classical physics allows populations of atoms or molecules to have nearly unlimited modes of vibration and movement (with corresponding degrees of freedom), quantum electrodynamics is a different story altogether.  Consider the electron orbits of a Hydrogen atom.  The allowed orbital values are discreet, and defined by Eq. 3.  Therefore electron orbits represent a population with very limited degrees of freedom (dimensions in phase

As a consequence of Eq. 3, an atom will only absorb (or emit) electromagnetic energy at those frequencies corresponding to the difference in energy between allowed orbits.  In a population of Hydrogen atoms at room temperature, the vast majority of electrons are in the orbit N = 1, and the effective temperature of the orbital population is very close to zero.  Now suppose we pass a controlled electric current through the Hydrogen atoms, thereby raising the majority of electrons into the orbit N = 2.  We now have a population with only 2 degrees of freedom (two dimensional phase space) N = 1, and N = 2.  Further, since the majority of electrons (greater than 50%) are in the orbit N = 2, the population of electron orbits is at a negative temperature (see figure 1 above), and therefore hotter than infinity.  In thermodynamics terms, this is known as a population inversion, and under the rules of classical thermodynamics, was considered a physical impossibility...

2.2.2

The Laser:

In 1960, based on the thermodynamic principal of population inversion, Theodore Maiman invented the laser (U.S. Pat 3,353,115).  An intense source of light or electric current is used to excite electron orbits into a population inversion.  The only way these electrons can cool down is to emit a beam of electromagnetic energy (photons) at a single wavelength, equal to the energy difference between electron orbits (2.2.1).  Since the population of photons in the laser beam is of one wavelength (monochromatic), they have exactly one degree of freedom, and as shown in (2.1.3), for any non-zero energy, when S = 0 (W = 1 in Eq. 1), T is infinite.

The laser uses the population inversion of electron orbits as a "daemon-like, trap door" to convert low temperature energy into a coherent beam of light, hot enough to burn a hole through the Sun

2.2.3

The second law:

The second law of thermodynamics states that:

"In any cyclic process, the entropy must either increase or remain the same".

Consider a steam engine.  Steam engines can not convert all of the energy contained in the boiler to useful work.  Some of the energy must be dumped into a condenser.  The reason for this prerequisite is that extracting energy from a boiler lowers the entropy of the boiler, however dumping a smaller quantity of energy into a condenser (at a lower temperature) raises the entropy of the condenser more than entropy was lowered by extracting the larger quantity of energy from the boiler (2.1.3, Eq. 2a).  In other words, a condenser is needed to meet the requirements of the second law of thermodynamics.

For steam engines, or any other engine that operates on the principal of heat extraction, the second law of thermodynamics IS absolute (much to the benefit of OPEC).  If steam engines could break the second law of thermodynamics, then a steam engine could convert all of the energy from a boiler operating at room temperature, without needing a lower temperature condenser to dump waste energy.

2.2.4

Inverted populations:

Consider an engine extracting energy from a boiler containing an inverted population of atoms or molecules.  Since the act of energy extraction, raises the entropy of the boiler (2.1.4, 2.2.1), this engine DOES NOT require a condenser, and this engine will convert ALL of the extracted energy into useful work.  In other words, ANY boiler operating on the right hand side of figure 1 (beyond 50% phase space occupancy), is also operating beyond the point of maximum entropy (disorder), and unlike a conventional boiler, entropy increases as energy is extracted from an inverted population boiler.  Therefore no other step is required to meet the condition imposed by the second law.

We have just uncovered a loop hole in the second law of thermodynamics.  This loop hole does NOT allow us to break the second law of thermodynamics.  Rather, the loop hole allows us to neatly "side step" the consequences of the second law, as it's traditionally understood to apply, with respect to heat driven engines.  In other words, an inverted population exhibits anti-entropic behavior.

Or in more poetic terms, when operating on an inverted population, the spirit of Maxwell's daemon LIVES!

2.3.1

Conclusions:

That inverted populations can be created (2.1.4, 2.2.1, 2.2.2).  That inverted populations exhibit anti-entropic behavior (2.2.4).  That inverted populations can be used to side step certain consequences of the second law of thermodynamics as it applies to heat driven engines (2.1.3, 2.1.4, 2.2.1, 2.2.2, 2.2.3, 2.2.4).  That when operating on an inverted population, the second law of thermodynamics DOES NOT preclude the existence of daemon-like "trap door" structures, as first envisioned by Maxwell (2.1.4, 2.2.1, 2.2.2, 2.2.4).  In summary, some scientists will claim that while my arguments are theoretically correct, they have no basis in physical reality.  I would invite these scientists to aim a high power laser at their head, then carefully examine the "theoretical hole" in their head.

End.

Magneto Thermodynamics, Part 2