|
3.1
Introduction:
In part two we saw how kinetic units of measure form an
ascending ladder. Here we shall discuss electrodynamic
units of measure and shall discover how these units form a
circular chain with no beginning or end. However, having
said that, we must still have some relation that ties
kinetic units of measure to electromagnetic units of
measure. The most convenient way to tie these two groups
together is through the definition of force on an electric
charge, produced by the electric field.
3.2.1
The electric field:
An electric field produces a force that acts upon any
electrically charged object, as shown in Eq. 1a.
|
[Eq. 1a]
|
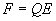 |
Where:
F = Force in Newtons.
Q = Electric charge in Coulombs.
E = Electric field.
Note: In part 3 of this paper we will redefine E as
the electric field instead of energy, and use J "joules" for
our energy variable.
Therefore, the electric field is defined by Eq. 1b.
|
[Eq. 1b]
|
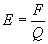 |
And since the fundamental units of force are
"meter-kilograms per second squared" (2.2.5), the
dimensional equivalent of the electric field in fundamental
units is:
|
[Eq. 1c]
|
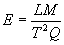 |
(dimensional equivalent of electric field in
fundamental units)
|
The unit of measure for a uniform electric field is "volts
per meter" or Newtons per Coulomb. By defining the electric
field as volts per meter, we also fix the dimensional
equivalent of "volt" in fundamental units as shown in Eq.
1d.
|
[Eq. 1d]
|
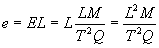 |
(dimensional equivalent of volt in fundamental
units)
|
Where:
e = Volts = Joules per Coulomb.
3.2.2
Force between electric charges:
The force between two electric charges is proportional to
the product of charge, and inversely proportional to the
square of their separation distance, as shown by Eq. 2a.
|
[Eq. 2a]
|
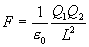 |
Where:
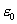 |
= Dielectric constant of free space in Farads per
meter.
|
The dielectric constant is required in order to make Eq. 2a
dimensionally balanced. In other words, from a dimensional
analysis view point: Q1*Q2 / L2,
does not equal force (L*M / T2).
Therefore the definition of the dielectric constant in
terms of fundamental units is derived as follows:
|
[Eq. 2b]
|
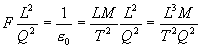 |
The dielectric constant is:
|
[Eq. 2c]
|
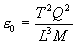 |
(dimensional equivalent of dielectric const. in
fundamental units)
|
The unit of measure for the dielectric constant is Farads
per meter, or in fundamental units, seconds squared-coulombs
squared per meter cubed-kilograms.
3.2.3
Generating an electric field:
Now that we have defined the dielectric constant in terms of
fundamental units, we can use that definition to examine the
process that creates the electric field. We know from 3.2.1
(above) that an electric field, when multiplied by an
electric charge, is equal to a force, and therefore the
electric field has the dimensional units of Newtons per
coulomb, and from 3.2.2 that electric charges exert a mutual
force upon each other. From these relationships, we surmise
that the dielectric constant multiplied by the electric
field is equal to the source of the electric field, as shown
in eq. 3.
|
[Eq. 3]
|
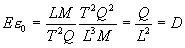 |
(dimensional equivalent of electric field
source)
|
Where:
D = Electric flux density in Coulombs per meter squared.
This result is somewhat surprising, since it implies there
is no such thing as "naked electric charge", only electric
charge per unit area (L2). In
other words, all electric charge is confined to surfaces (a
sphere for example).
3.2.4
The magnetic field:
The force experienced by an electric charge moving through a
magnetic field (B) is proportional to the quantity of
charge, the magnetic field strength, and the velocity of
movement. Furthermore this force manifests at right angles
to both the direction of movement and magnetic field vector.
Eq. 4a shows this relationship in mathematical form.
|
[Eq. 4a]
|
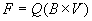 |
Ignoring the vector cross product, we get Eq. 4b.
|
[Eq. 4b]
|
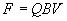 |
Therefore, we can define the magnetic field in terms of
force, charge, and velocity as shown in Eq. 4c.
|
[Eq. 4c]
|
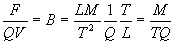 |
(dimensional equivalent of magnetic field)
|
Where:
B = Magnetic field in Teslas or kilograms per
coulomb-seconds
Another way to view this result is that a magnetic field is
a velocity deficient electric field, as shown in Eq. 4d
(velocity transforms a magnetic field into an electric
field).
|
[Eq. 4d]
|
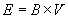 |
3.2.5
Electric charge in motion:
If we take our electric flux (D) from 3.2.3 (above) and give
it a proper motion, the result is a magnetic flux (H) shown
in Eq. 5a.
|
[Eq. 5a]
|
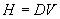 |
And from the dimensional analysis view point, we have:
|
[Eq. 5b]
|
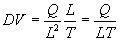 |
(dimensional equivalent of magnetic flux)
|
Where:
H = Magnetic flux in Webbers or coulombs per meter-seconds.
Since electric current (amps) is defined as Coulombs per
second, we can also view magnetic flux (H) as "amps per
meter".
3.2.6
Generating a magnetic field.
In 3.2.4 we defined the magnetic field, and in 3.2.5 we
defined the magnetic flux. All that is left is to define
the relationship between the magnetic field, and the
magnetic flux that creates it. This relationship is shown in
Eq. 6a.
|
[Eq. 6a]
|
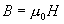 |
Where:
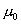 |
= Paramagnetic constant of free space in Henries
per meter.
|
The paramagnetic constant is required in order to make the
flux and the field it generates dimensionally balanced.
Therefore we define the paramagnetic constant as the ratio
of magnetic field strength to magnetic flux, as shown in Eq.
6b.
|
[Eq. 6b]
|
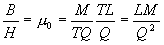 |
(dimensional equivalent of paramagnetic
constant)
|
3.3.1
The endless loop:
|
E
|
 |
|
Sec. 3.2.1
|
|
Multiplied by
|
 |
|
Sec. 3.2.2
|
|
Equals
|
|
D
|
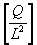 |
|
Sec. 3.2.3
|
|
|
Equals
|
|
|
|
Multiplied by
|
|
V
|
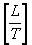 |
|
Sec. 2.2.3
|
|
|
Dimensional
equivalent
shown in
brackets
|
|
|
V
|
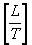 |
|
Sec. 2.2.3
|
|
|
Multiplied by
|
|
|
|
Equals
|
|
B
|
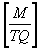 |
|
Sec. 3.2.4
|
|
Equals
|
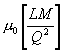 |
|
Sec. 3.2.6
|
|
Multiplied by
|
|
H
|
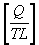 |
|
Sec. 3.2.5
|
|
As mentioned in the introduction (3.1), the electromagnetic
units of measure form a circular chain or endless loop
(shown above). At first this result may seem surprising but
it is precisely this set of relationships that lead to
electromagnetic wave propagation.
3.3.2
Other derivatives:
While the above set of electromagnetic units of measure are
arguably the most widely used, many other units of measure
may be derived from the electromagnetic units chain. Among
the more useful are:
The speed of light in free space is calculated from the
paramagnetic (also known as the permeability of free space)
and dielectric constants of free space. The local speed of
light in any media, may be calculated by substituting the
local values of paramagnetic and dielectric polarization.
This relationship is shown in Eq. 7.
|
[Eq. 7]
|
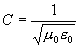 |
The Poynting vector "P" is calculated as a cross product of
the electric field and magnetic flux as shown in Eq. 8.
|
[Eq. 8]
|
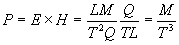 |
(dimensional equivalent of Poynting vector)
|
In Eq. 9 we discover that mass itself results from
electromagnetic rotation in 3 spatial dimensions.
|
[Eq. 9]
|
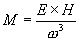 |
Where:
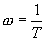 |
(radians per second)
|
Finally, since both mass and the speed of light can be
derived from electromagnetic phenomena, we could choose to
rewrite Einstein's famous equation by combining Eq. 7 and
Eq. 9, as shown in Eq. 10.
|
[Eq. 10]
|
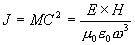 |
3.4
Summary:
As we have seen, dimensional analysis is a tool of
astounding power. It provides the physicist with a reliable
method to understand the many and varied relationships of
physical mathematics, as well as giving us a glimpse
directly into the inner workings of the universe. While
this tutorial is finished, the journey is far from over...
End.
Dimensional Analysis - Part 3
|