|
1.1
Introduction:
Algebra, as it applies to dimensional analysis, concerns
itself with the proper manipulation of simple and complex
units of measure, under the operations of addition,
subtraction, multiplication, and division. Most algebra is
taught as concerning itself with solving equations to
determine numeric values. But consider...
Suppose an equation solves to a numeric value of five.
Five what?
Five oranges?
Five nuclear bombs?
Five temple virgins?
Without dimensional analysis, we don't know what the number
"five" is describing!!!!
If we don't know what units the number "five" is measuring,
and we build some device based on this equation what will
happen? We could get "five" nukes instead of "five"
virgins. And unless you're a terrorist, this could ruin
your day, not to mention your entire city.
The rest of dimensional analysis part 1 outlines the rules
for construction and/or deconstruction of units of measure.
1.2.1
Numbers:
Numeric values are dimensionless. They do NOT change the
amount of units involved. An example is shown in Eq. 1.
|
[Eq. 1]
|
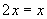 |
Numerically Eq. 1 is WRONG. However, since dimensional
analysis concerns itself exclusively with units,
not numeric values, this equation is "dimensionally
correct". There is one exception to this rule, and that is
an exponential unit such as x2.
When a number is used as an exponent (of some unit of
measure) it does change the quantity of units. An example
is shown in Eq. 2.
|
[Eq. 2]
|
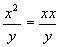 |
1.2.2
Addition and subtraction:
The operations of addition and subtraction do not change the
amount of units involved. Equations Eq. 3 and Eq. 4 show
some examples.
|
[Eq. 3]
|
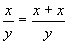 |
|
[Eq. 4]
|
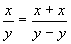 |
Again, I must stress, these equations are numerically WRONG,
but dimensionally CORRECT. Remember, we are not concerned
with "numbers" here. We are concerned with the UNITS of
measure (oranges, nukes or virgins).
1.2.3
Multiplication and division:
The operations of multiplication and division do
change the amount of units involved. This section represent
the "meat and potatoes" of the subject.
Some examples:
Lets give the variables a, b, and c the following units of
measure:
a = oranges.
b = virgins.
c = nukes.
Therefore:
|
[Eq. 5]
|
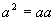 |
(oranges squared)
|
Assume Z is a complex quantity composed of:
|
[Eq. 6]
|
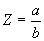 |
(oranges per virgin)
|
Then we have as our dimensional results:
|
[Eq. 7]
|
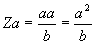 |
(oranges squared per virgin)
|
|
[Eq. 8]
|
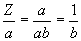 |
(per virgin)
|
|
[Eq. 9]
|
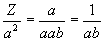 |
(per orange-virgins)
|
|
[Eq. 10]
|
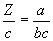 |
(oranges per virgin-nuke)
|
|
[Eq. 11]
|
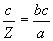 |
(virgin-nukes per orange)
|
Notice that in Eq. 11, placing Z below the division platform
has the effect of inverting it's units (oranges per virgin).
Just to make sure this is true, lets do the math:
a = 5 (oranges)
b = 2 (virgins)
c = 10 (nukes)
|
So:
|
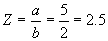 |
(oranges per virgin)
|
|
Therefore:
|
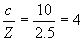 |
(but 4 what???)
|
Now lets do it like the right side of Eq. 11:
|
We get:
|
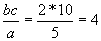 |
(and now we know it's 4 virgin-nukes per orange)
|
Both the left and right sides of Eq. 11 yield the proper
numeric result, but the right side of Eq. 11 shows us what
the units of measurement are with a single glance.
1.2.4
Cancellation:
When some unit of measure appears both above and below the
division platform, it can be canceled out, only to the equal
amounts of the unit. Some examples:
Assume the same units and variable names as section 1.2.3
(above).
Then cancellation results in:
|
[Eq. 12]
|
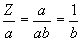 |
(per virgin)
|
|
[Eq. 13]
|
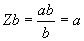 |
(oranges)
|
|
[Eq. 14]
|
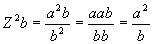 |
(oranges squared per virgin)
|
|
[Eq. 15]
|
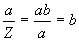 |
(virgins)
|
|
[Eq. 16]
|
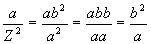 |
(virgins squared per orange)
|
1.3
Summary:
Thanks to dimensional analysis, we can freely mix oranges,
virgins, and nukes, with a high degree of precision and
assurance that our results will not produce unintended side
effects (a great comfort to our wives, neighbors, and local
emergency response personnel). In part 2, we shall apply
dimensional analysis to kinetics.
End.
Dimensional Analysis - Part 1
|